Об использовании амплитуд, измеренных коррелятором

Коррелятор Радиогелиографа измеряет ковариацию (кросс-корреляцию) двух 4-битовых или 1-битовых сигналов от пары антенн. Назовем эти сигналы квантованными сигналами, а устройство, получающее эти сигналы из исходных - квантователь. Разрядность квантователя, вид его характеристики и вес одного разряда задаются при инициализации цифровых приемников Радиогелиографа перед началом наблюдений. Для обозначения квантованных сигналов будем использовать символ $\hat{ }$. Так как коррелятор измеряет ковариации всех пар антенн, то часть из них являются автокорреляциями или дисперсиями квантованных сигналов ${\hat{\sigma}_x}^2$, где x - индекс антенны, $\hat{\sigma}$ - среднеквадратичное отклонение. Тогда квантованный коэффициент корреляции определяется как $\hat{\rho}=\frac{cov\left(\hat{x}\hat{y}\right)}{\hat{\sigma}_x\hat{\sigma}_y}$. В случае 1-битового квантователя $\hat{\sigma}_x=x=\hat{\sigma}_y=y=1$, $\hat{\rho}=cov\left(\hat{x}\hat{y}\right)$ и истинный коэффициент корреляции определяется коррекцией ван Флека $\rho=sin\left(\frac{\pi}{2}\hat{\rho}\right)$. В случае многобитового квантователя истинный коэффициент корреляции равен $\rho = gV\left(\hat{\rho},\sigma_x,\sigma_y,\right)$, где gV обобщенная коррекция ван Флека. Заметим, что для вычисления истинного коэффициента корреляции из измеренных ковариаций необходимо сначала вычислить истинные дисперсии $\sigma^2$. На рисунке показаны модельные зависимости квантованных коэффициентов корреляции для разрядност 1 и 4. Видно, что 4-битовый коэффициент корреляции отличается от истинного 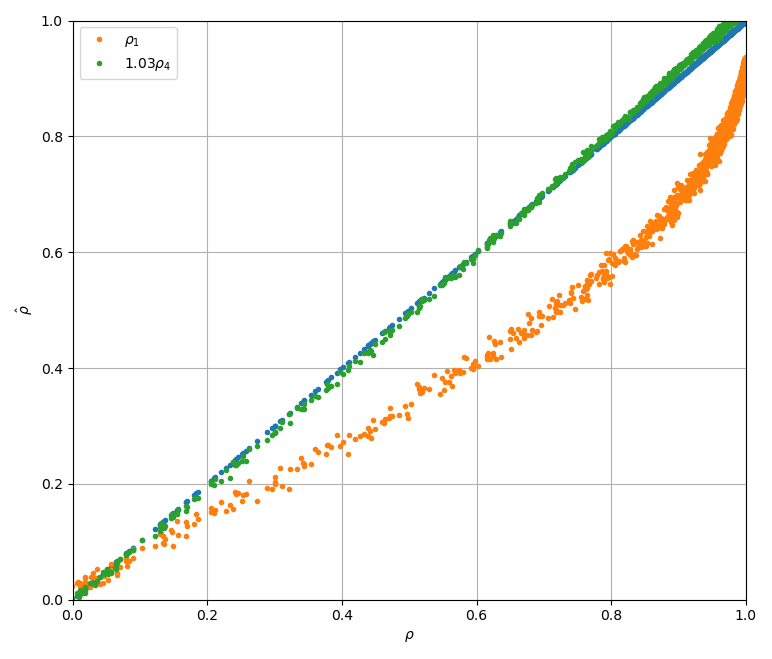 более чем на 3% в области значений больше 0.8. Поэтому в большинестве случаев можно использовать 4-битовый коэффициент корреляции и без обобщенноей коррекции ван Флека. Хотя, для исследования всех событий и для достижения максимальной достоверности обобщенная коррекция ван Флека необходима. Получить 4-битовый коэффициент корреляции из набора ковариаций, записанных коррелятором можно следующим образом. Данные ковариаций находятся в колонках 'vis_lcp' и 'vis_rcp' исходных фитсов. Данные квантованных дисперсий (амплитуд) находятся в колонках 'amp_lcp_c' и 'amp_rcp_c'. Допустим мы обрабатываем ковариацию (видность) антенн A и B дл левой круговой поляризации. Тогда $\hat{\rho}{AB} = vislcp{[A,B]} / \sqrt{amp_lcp_c[A]}\sqrt{amp_lcp_c[B]}$.